震源時間関数に関して
1.Moment-rate型関数
(Moment-rate
time history) :![]() と表記
と表記
![]() でゼロ、常に正、
でゼロ、常に正、![]() で積分を行うと1.0となる、などの性質をもち、断層面の滑り速度関数に
で積分を行うと1.0となる、などの性質をもち、断層面の滑り速度関数に![]() をかけたものと同等。
をかけたものと同等。
2.Moment型関数
(Moment
time history) :![]() と表記
と表記
Moment-rate
time historyを時間積分したもので、![]() でゼロ、
でゼロ、![]() で1.0、単調増加関数、などの性質をもつ。断層面の滑りに
で1.0、単調増加関数、などの性質をもつ。断層面の滑りに![]() をかけたものと同等。
をかけたものと同等。
3.その他の関数 :![]() と表記
と表記
Ricker waveletなど。断層運動とは関係づけられないが、数値実験等でよく用いられる。
○震源の導入法による関数系の選択
速度応力の食い違い格子の差分法において断層型点震源の導入法には、応力に外部力を加える方法(SSF)、速度に外部力を加える方法(VSF)、source boxを用いる方法、3つの方法がある。GMSにおいては1番目と2番目が選択できるが。SSFでは、Moment-rate型関数を用い、VSFではMoment型関数を用いる。VSFでは、理論上は釣り合ってキャンセルアウトする外部力がかかり続けることになる。わずかな誤差であっても永久に媒質が移動し続けるような外部力が加わり続けることは望ましくないため、通常はSSFを用いることを推奨する。
○時間シフトに関して
差分法では用いる震源時間関数は、できる限りなめらか関数であることが望ましい。従って、関数値はゼロから立ち上がる必要がある。
GMSでは、ほとんどの関数に対して、![]() で最大値をとる関数とnon-shiftedの関数、
で最大値をとる関数とnon-shiftedの関数、![]() で(事実上)ゼロとなるように適当な時間シフトを行なったshiftedの関数を用意している。
で(事実上)ゼロとなるように適当な時間シフトを行なったshiftedの関数を用意している。
通常はshiftedの関数を用いればよいが、時間シフトが卓越周期・characteristic frequency (以下![]() 等)に依存するため、複数の
等)に依存するため、複数の![]() 等を混在させる場合などには注意が必要である。
等を混在させる場合などには注意が必要である。
sourcetimefunction.txt
# Last modification:2003/01/24 by Shin Aoi
Ricker wavelet,Center frequency[Hz],0.5
dummy
Ricker wavelet(shifted),Center frequency[Hz],0.5
dummy
Gabor wavelet, fp[Hz],1,gama,1,psi/pi,1
dummy
Gabor wavelet(shifted), fp[Hz],1,gama,1,psi/pi,1
dummy
Boxcar, 1/rise_time[1/s],1
Int of Boxcar, 1/rise_time[1/s],1
Boxcar(shifted), 1/rise_time[1/s],1
Int of Boxcar(shifted), 1/rise_time[1/s],1
Triangle, 1/rise_time[1/s],1
Int of Triangle, 1/rise_time[1/s],1
Triangle(shifted), 1/rise_time[1/s],1
Int of Triangle(shifted), 1/rise_time[1/s],1
Diff of Smoothed Ramp, 1/rise_time[1/s],1
Smoothed Ramp, 1/rise_time[1/s],1
Diff of Smoothed Ramp(shifted), 1/rise_time[1/s],1
Smoothed Ramp(shifted), 1/rise_time[1/s],1
Sin function, 1/rise_time[1/s],1,alpha,1
Int of Sin function, 1/rise_time[1/s],1,alpha,1
Sin function(shifted), 1/rise_time[1/s],1,alpha,1
Int of Sin function(shifted), 1/rise_time[1/s],1,alpha,1
diff of SCEC_3DVP, 1/time constant[1/s], 0.5
SCEC_3DVP, 1/time constant[1/s], 0.5
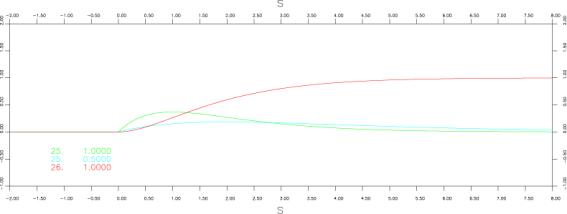
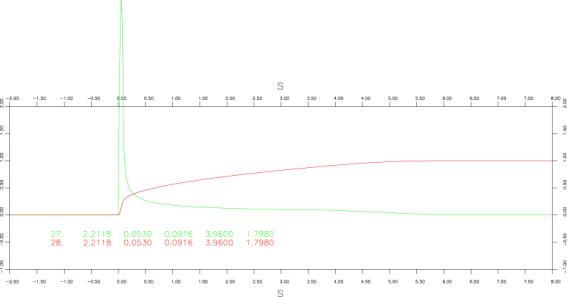
Nakamura&Miyatake(2000), Vm[m/s], 2.2118, td[s], 5.3E-2, tb[s], 9.16108E-2, tr[s], 3.96, amp, 1.7980
Int of Nakamura&Miyatake(2000), Vm[m/s], 2.2118, td[s], 5.3E-2, tb[s], 9.16108E-2, tr[s], 3.96, amp, 1.7980
●Ricker wavelet
iswstf = 1 (iswstf = 2は未定義)
定義式:
![]()
パラメター:1つ
stfprm(1):![]() :characteristic frequency[Hz](パルス幅の逆数に相当する)
:characteristic frequency[Hz](パルス幅の逆数に相当する)
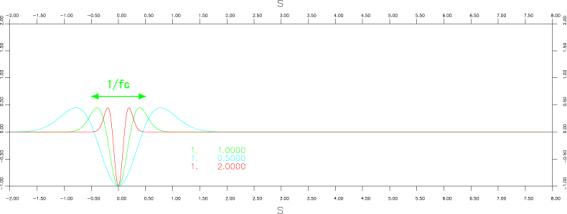
注意:微分不可能点:なし
:![]() 以上タイムシフトして使用すること。
以上タイムシフトして使用すること。
●Ricker wavelet(shifted)
iswstf = 3 (iswstf = 4は未定義)
定義式:
![]()
パラメター:1つ
stfprm(1):![]() :characteristic frequency[Hz](パルス幅の逆数に相当する)
:characteristic frequency[Hz](パルス幅の逆数に相当する)
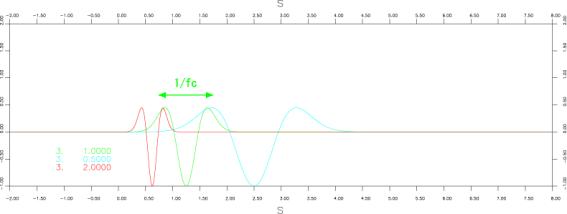
注意:微分不可能点:なし
:![]() だけタイムシフトすることにより、関数の頭がおおむねゼロになっている。
だけタイムシフトすることにより、関数の頭がおおむねゼロになっている。
●Gabor wavelet
iswstf = 5 (iswstf = 6は未定義)
定義式:
![]()
パラメター:3つ
stfprm(1):![]() :characteristic [predominant] frequency[Hz](関数の卓越周波数)
:characteristic [predominant] frequency[Hz](関数の卓越周波数)
stfprm(2):![]() :width of the signel[ ](関数の継続時間をコントロールする変数)
:width of the signel[ ](関数の継続時間をコントロールする変数)
stfprm(3):![]() :phase shift[ ] (このパラメタの
:phase shift[ ] (このパラメタの![]() 倍の
倍の![]() だけ位相がシフトされる)
だけ位相がシフトされる)
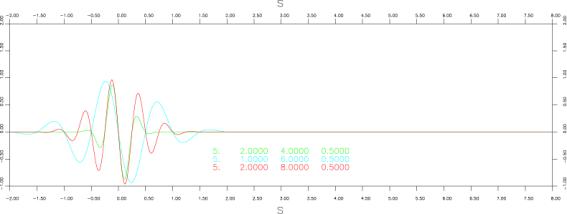
注意:微分不可能点:なし
:![]() 以上タイムシフトして使用すること。
以上タイムシフトして使用すること。
●Gabor wavelet(shifted)
iswstf = 7 (iswstf = 8は未定義)
定義式:
![]()
パラメター:3つ
stfprm(1):![]() :characteristic [predominant] frequency[Hz](関数の卓越周波数)
:characteristic [predominant] frequency[Hz](関数の卓越周波数)
stfprm(2):![]() :width of the signel[ ](関数の継続時間をコントロールする変数)
:width of the signel[ ](関数の継続時間をコントロールする変数)
stfprm(3):![]() :phase shift[ ](このパラメタの
:phase shift[ ](このパラメタの![]() 倍の
倍の![]() だけ位相がシフトされる)
だけ位相がシフトされる)
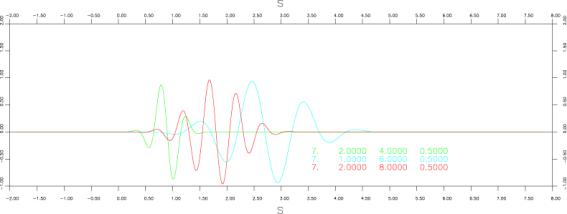
注意:微分不可能点:なし
:![]() だけタイムシフトすることにより、関数の頭がおおむねゼロになっている。
だけタイムシフトすることにより、関数の頭がおおむねゼロになっている。
●箱形(Boxcar function)
iswstf = 9 and 10
定義式:
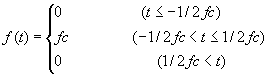
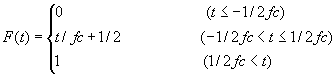
パラメター:1つ
stfprm(1):![]() :底辺の幅の逆数[Hz]
:底辺の幅の逆数[Hz]
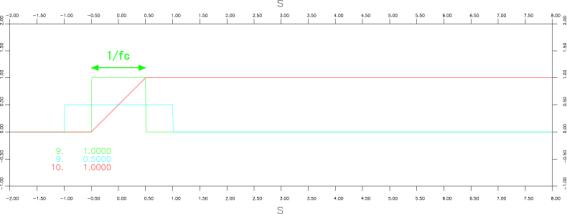
注意:不連続点:![]() 。滑り関数においても微分不可能点となる。
。滑り関数においても微分不可能点となる。
:![]() 以上タイムシフトして使用すること。
以上タイムシフトして使用すること。
:立ち上がりが不連続なので、差分計算で不安定を起こす可能性が大きい。
使用を推奨しない。
●箱形(Boxcar function) (shifted)
iswstf = 11 and 12
定義式:
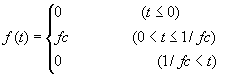

パラメター:1つ
stfprm(1):![]() :底辺の幅の逆数[Hz]
:底辺の幅の逆数[Hz]
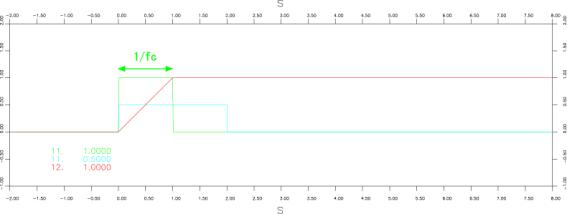
注意:不連続点:![]() 。滑り関数においても微分不可能点となる。
。滑り関数においても微分不可能点となる。
:![]() だけタイムシフトすることにより、関数の頭がゼロになっている。
だけタイムシフトすることにより、関数の頭がゼロになっている。
:立ち上がりが不連続なので、差分計算で不安定を起こす可能性が大きい。
使用を推奨しない。
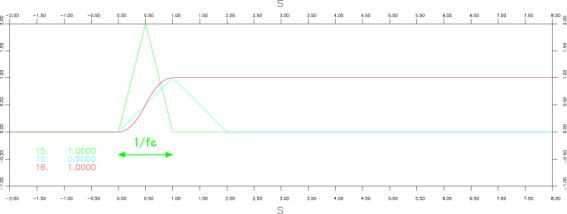
●三角形(Triangle function)
iswstf = 13 and 14
定義式:![]()
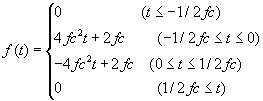
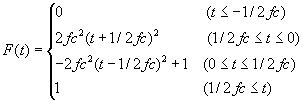
パラメター:1つ
stfprm(1):![]() :三角形の底辺の幅の逆数[Hz]
:三角形の底辺の幅の逆数[Hz]
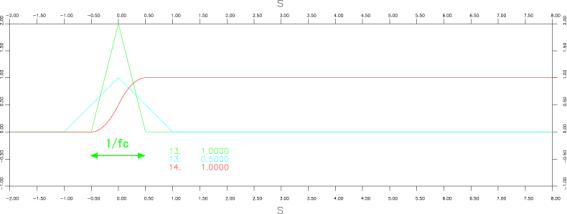
注意:微分不可能点:![]()
:![]() 以上タイムシフトして使用すること。
以上タイムシフトして使用すること。
●三角形(Triangle function) (shifted)
iswstf = 15 and 16
定義式:
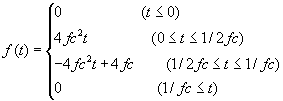
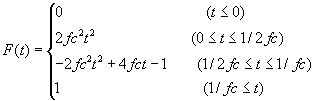
パラメター:1つ
stfprm(1):![]() :三角形の底辺の幅の逆数[Hz]
:三角形の底辺の幅の逆数[Hz]
注意:微分不可能点:![]()
:![]() だけタイムシフトすることにより、関数の頭がゼロになっている。
だけタイムシフトすることにより、関数の頭がゼロになっている。
●Smoothed ramp function
iswstf = 17 and 18
定義式:
![]()
![]()
パラメター:1つ
stfprm(1):![]() :characteristic frequency[Hz](パルス幅の逆数に相当する)
:characteristic frequency[Hz](パルス幅の逆数に相当する)
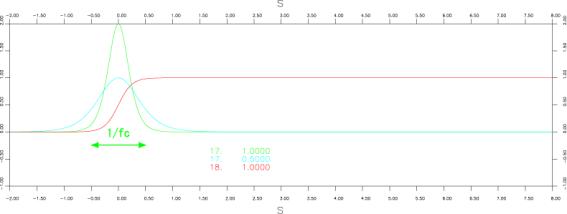
注意:微分不可能点:なし
:![]() 以上タイムシフトして使用すること(
以上タイムシフトして使用すること(![]() では足りない)。
では足りない)。
●Smoothed ramp function(shifted)
iswstf = 19 and 20
定義式:
![]()
![]()
パラメター:1つ
stfprm(1):![]() :characteristic frequency[Hz](パルス幅の逆数に相当する)
:characteristic frequency[Hz](パルス幅の逆数に相当する)
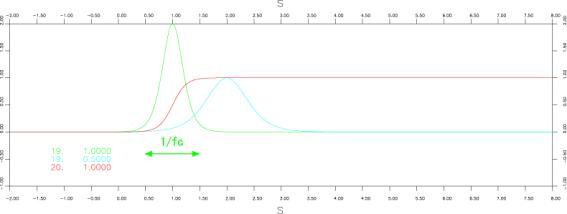
注意:微分不可能点:なし
:![]() だけタイムシフトすることにより、関数の頭がおおむねゼロになっている。
だけタイムシフトすることにより、関数の頭がおおむねゼロになっている。
●三角関数(Sin function)
iswstf = 21 and 22
定義式:
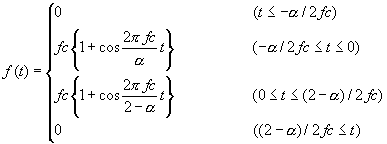
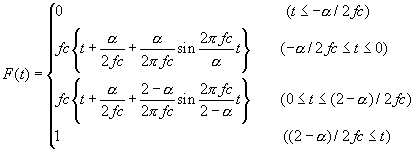
パラメター:2つ
stfprm(1):![]() :底辺の幅の逆数[Hz]
:底辺の幅の逆数[Hz]
stfprm(2):![]() :前半と後半の三角関数の幅の比(
:前半と後半の三角関数の幅の比(![]() )
)
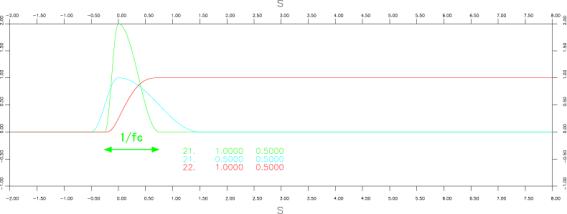
注意:微分不可能点:なし
:![]() 以上タイムシフトして使用すること。
以上タイムシフトして使用すること。
●三角関数(Sin function) (shifted)
iswstf = 23 and 24
定義式:
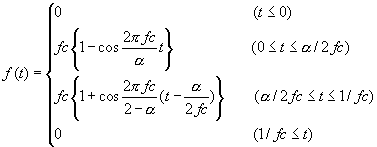
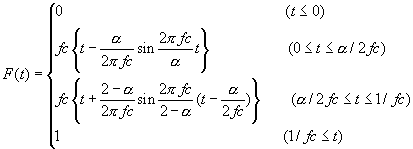
パラメター:2つ
stfprm(1):![]() :底辺の幅の逆数[Hz]
:底辺の幅の逆数[Hz]
stfprm(2):![]() :前半と後半の三角関数の幅の比(
:前半と後半の三角関数の幅の比(![]() )
)
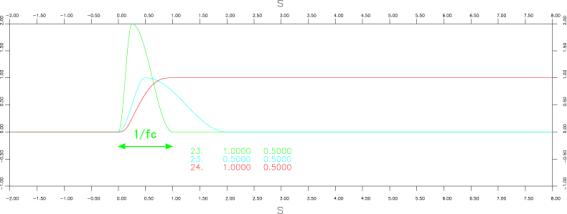
注意:微分不可能点:なし
:![]() だけタイムシフトすることにより、関数の頭がゼロになっている。
だけタイムシフトすることにより、関数の頭がゼロになっている。
●SCEC_3DVP
iswstf = 25 and 26
定義式:
Moment-rate time history
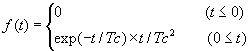
Moment time history
![]()
パラメター:1つ
stfprm(1):![]() :
:![]() [Hz]。ただし、
[Hz]。ただし、![]() の物理的意味は不明。
の物理的意味は不明。
注意:微分不可能点:![]()
:SCEC/PG&E/PEER 3D VERIFICATION PROBLEMS, Working Draft (July 26, 2000)で使用されているもの。一般的な関数であるかどうかは、不明。
:卓越周期は明らかに、![]() より長い。物理的意味不明。
より長い。物理的意味不明。
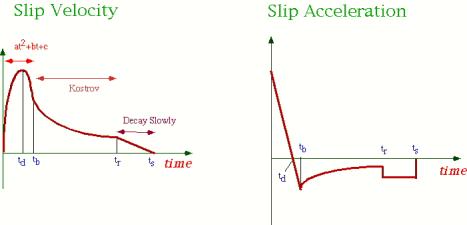
●中村・宮武 (2000, 地震、第53巻、pp1-9)
iswstf = 27 and 28
定義式:
パラメター:5つ
stfprm(1):![]() :最大すべ速度[m/s]
:最大すべ速度[m/s]
stfprm(2):![]() :最大滑り速度に達するまでの時間(2次関数の極大点)[s]
:最大滑り速度に達するまでの時間(2次関数の極大点)[s]
stfprm(3):![]() :2次関数からKostrov型関数に移行するまでの時間[s]
:2次関数からKostrov型関数に移行するまでの時間[s]
stfprm(4):![]() :Kostrov型関数から1次関数(減速部分)に移行するまでの時間[s]
:Kostrov型関数から1次関数(減速部分)に移行するまでの時間[s]
stfprm(5):amp:積分の終端値が1になるように調整するためのファクター[ ]
注意:微分不可能点:![]()
:![]() は下記のプログラム(http://www.eri.u-tokyo.ac.jp/miyatake/SlipFunc-Prog.htmlより引用)にて決める。
は下記のプログラム(http://www.eri.u-tokyo.ac.jp/miyatake/SlipFunc-Prog.htmlより引用)にて決める。
:ampは、モーメントが1.0になるように決定する。
 (http://www.eri.u-tokyo.ac.jp/miyatake/SlipFunc-Prog.htmlより引用)
(http://www.eri.u-tokyo.ac.jp/miyatake/SlipFunc-Prog.htmlより引用)
subroutine vslip(tm,rate,ndt,nt,slip,td,vm,tr,ts) dimension rate(ndt),tm(ndt) error = 1.0e-5 Am = 2.0 * Vm / td isw = 1 h = td x = td*1.01 call tslip(y1,slip,x ,Vm,Am,td,tr,ts,b,c,ar,eps) 1 call tslip(y2,slip,x+h,Vm,Am,td,tr,ts,b,c,ar,eps) if(y1*y2.gt.0.0) then x = x + h y1 = y2 if(isw.eq.1) goto 1 endif h = h / 2.0 isw = 2 if(h.gt.error) goto 1 tb = x do k=1,nt if(tm(k).le.tb) then v = Am * tm(k) * ( 1.0 - 0.5 * tm(k) / td ) endif if(tm(k).gt.tb.and.tm(k).le.tr) then v = b / sqrt( tm(k) - eps) endif if(tm(k).gt.tr.and.tm(k).le.ts) then v = c - ar * ( tm(k) - tr ) endif if(tm(k).gt.ts) v = 0 if(tm(k).lt. 0) v = 0 rate(k) = v enddo return end c**************************************** subroutine tslip(res,target,tb,Vm,Am,td,tr,ts,b,c,ar,eps) eps = tb + tb / 2 * (1.0-tb/td/2.0)/(1.0-tb/td) if(eps.gt.tb) eps = tb b = -2.0 * Am * ( 1.0 - tb / td ) * ( tb - eps ) ** 1.5 c = b / sqrt(tr-eps) ar = c / ( ts - tr ) f1 = Am / 2.0 * tb * tb - Am / 6.0 * (tb**3) / td f2 = 2.0 * b * ( sqrt(tr-eps) - sqrt(tb-eps) ) f3 = c / 2.0 * ( ts - tr ) res = f1 + f2 + f3 - target return end
|